My research interests are in condensed matter physics, in particular in strongly correlated low-dimensional many-body systems. I am mainly interested in the dissipative and out-of-equilibrium dynamics of atomic gases. I am also interested in exact solutions in many-body systems, namely integrable and conformal models, for which I study the entanglement properties in the low-energy spectrum.
|
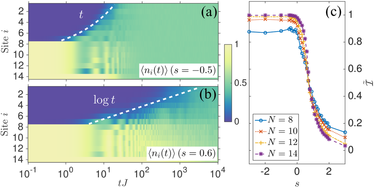
Phys. Rev. B 92, 100305(R) (2015). Different dynamical properties in the ergodic (a) and MBL (b) phases for a translation invariant system. Excitations spread logarithmically in time in the MBL phase. The MBL transition is evident in the stationary value of the inverse partecipation ratio (c).
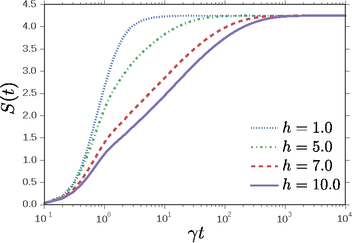
arXiv:1510.04634 (2015). The von Neumann entropy quantifies the heating of a system in contact with an infinite temperature bath. In the MBL phase this heating progresses logarithmically slowly, implying exponentially large relaxation timescales.
|
Many-body localization
The wave function of an electron subject to quenched disorder is very far from being a plane wave, and has an envelope which decays exponentially in space. This feature goes under the name of Anderson Localization and has strong implications on transport properties, leading to an insulating phase for strong enough disorder.
The aim of Many-Body Localization (MBL) is to extend this concepts to many-body interacting systems. In an interacting system an insulating and conducting phase are separated by a so called MBL phase transition. These phases display very different dynamical properties, the MBL phase breaking ergodicity and keeping memory of the initial state in the steady state. A particularly interesting open problem is understanding how this ergodicity breaking is achieved for systems without disorder (translation invariant). While there have been several numerical indications of ergodicity breaking for translation invariant systems, it is still a matter of debate if a proper MBL phase is present in absence of disorder, or a transient MBL behaviour is followed by the restoration of ergodicity on long timescales. Another recent and open field of research is the study on how dissipation affects the ergodic properties in the MBL phase. This problem is of particular appeal if one wants to engineer an experimental realization of MBL, as the effects of an imperfect isolation of the system have to be taken into account. The exchange of heat with the environment will eventually induce ergodicity on long timescales and therefore destroy the MBL state. I am studying the mechanisms and timescales at which this happens. |
Dissipative atomic gases
.In recent years, there has been a growing interest in under-
standing dynamical phase transitions in the context of driven open many-body quantum systems. Progress in the manipulation of ultracold atoms has made it possible to access and explore many-body phenomena under precisely controllable experimental conditions. Particularly interesting is the case of Rydberg gases, i.e., atomic clouds in which atoms are laser-excited to high-lying energy levels. The population of such orbitals in turn leads to a considerable increase in the interaction strength. In this context an open problem is the emergence of bistability in the dissipative regime. This effect led to the experimental observation of a bimodal distribution of the excitation density in a dissipative Rubidium gas, and optical bistability in a thermal Cesium vapour. These examples are well studied with a mean-field approach, which predicts the universality class and spinodal physics. Equally interesting is the case in which the physics of a dissipative Rydberg gas is explained by a non-equilibrium universality class. One of the most fundamental and well-studied universality classes of this kind is directed percolation (DP). Despite its simplicity and robustness has been very difficult to identify clear signs of DP universality in physical systems. In fact the first convincing signatures of DP criticality were found as late as 2007 in a two-dimensional turbolent liquid crystals. Lately a proposal to observe DP universality in a one to three-dimensional Rydberg gas has been pushed forward. |
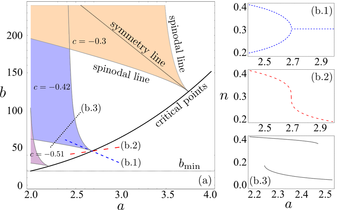
Phys. Rev. Lett. 113, 210401 (2014). The mean-field phase diagram of the steady state of a Rydberg gas subject to decay and decoherence presents regions of bistability delimited by so called spinodal lines (a). Entering this region along the different directions (b.1), (b.2) and (b.3) allows to identify the universality of this gas to be Model A (Ising with no conserved dynamical quantities).
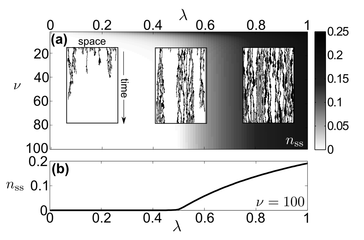
New J. Phys. 17 072003 (2015). Directed percolation transition in the steady population of excitations in a dissipative Rydberg gas subject to strong dephasing.
|
|
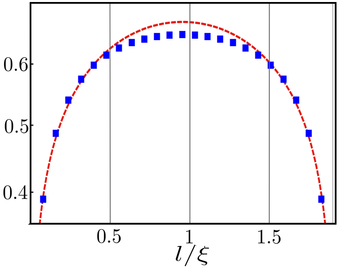
J. Phys. A: Math. Theor. 48 (2015). Entanglement entropy for a finite chain discretization of the non-unitary Yang-Lee minimal model. The non-unitary conformal behaviour is tested against numerical data, showing a good agreement for lengths of the block considerably smaller than the correlation length.
|
Entanglement in integrable and Conformal Field Theories
A many-body system close to a second order phase transition is subject to collective phenomena at all distance scales. This makes the correlation length of such a system very large and its physics scale invariant. A powerful and elegant analytical tool to describe this scenario is Conformal Field Theory. CFT is particularly powerful in two dimensions, where it allowed to a complete classification of universality classes.
A great deal of critical one-dimensional quantum many-body systems fall in a 2D CFT universality class and an analytical study is generally possible. Of particular interest are the entanglement properties of a quantum system, e.g. the entanglement present in the ground state. Since the ground state of a many-body system is generally a pure state the usual practice is to divide the system into two parts, and quantify the entanglement between them with the von Neumann entropy. This brought to the discovery that entanglement entropy follows an area law, e.g. increases with the boundary between the two regions. This law is "softly" broken in one dimension, where the entanglement entropy increases logarithmically with the block length. The rate of increase of the entanglement entropy is given by the central charge, which quantifies the microscopic degrees of freedom of a system. More involved is the case of non-unitary CFT, or all those cases for which the ground state of a physical system does not correspond to the vacuum of the CFT. In these case it has demonstrated that it is the effective central charge to play the role of the central charge in the unitary case. Another interesting development is the connection between entanglement entropy and Zamolodchikov c-function. The c-function describes how the central charge flows along the renormalization group, where the system is non-critical. A particularly interesting open question is whether it is possible to obtain a c-function from the entanglement entropy. |